动态规划
0.1背包 理论基础

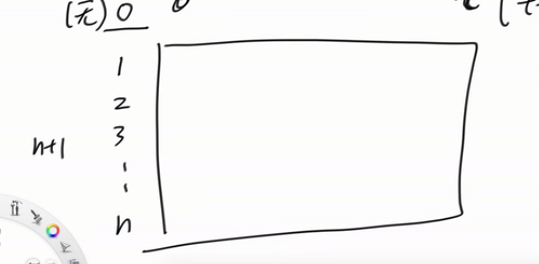
二维表 行代表选取0-n 多少物品
列代表 最大容量
最后需要的是最后一个格子的值
普通版本
import java.util.*;
public class Main {
public static void main(String[] args) { // 1. 读取输入
Scanner sc = new Scanner(System.in);
// 读取第一行
int M = sc.nextInt(); // 材料种类
int N = sc.nextInt(); // 行李空间大小
// 读取第二行:每种研究材料的占用空间
int[] weights = new int[M+1];
for (int i = 1; i <= M; i++) {
weights[i] = sc.nextInt();
}
// 读取第三行:每种研究材料的价值
int[] values = new int[M+1];
for (int i = 1; i <= M; i++) {
values[i] = sc.nextInt();
}
// 2. 定义一维dp数组,dp[j]表示容量为j时可以获取的最大价值
int[][] dp = new int[M+1][N + 1];
for (int i=1;i<=M ;i++ ){
for(int j=0;j<=N;j++){
dp[i][j]=dp[i-1][j];
if(j - weights[i] >= 0) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - weights[i]] + values[i]);
}
}
}
System.out.println(dp[M][N]);
}}每一个格子 依靠的其实是该格子的上一个格子 和上一行格子左边的我某个格子
注意:要判断当前容量能否放得下第i个物品
压缩版本
用一个一维数组,我们不用去保存每一行的值,dp一维数组我们可以动态的滚动,注意要从右往左更新,因为格子依靠的是上一行和其上一行左边格子的值,从右往左时,上一行及其左边的值还没有被覆盖。
如果从左往右,左边的值已经被覆盖。
注意,当j<weights[i]时,我们就可以跳出该次循环了,因为接下来j--,j一定还是小于当前物品容量的,我们跳出循环,默认dp[J]就等于其上一行的值。
import java.util.*;
public class Main {
public static void main(String[] args) { // 1. 读取输入
Scanner sc = new Scanner(System.in);
// 读取第一行
int M = sc.nextInt(); // 材料种类
int N = sc.nextInt(); // 行李空间大小
// 读取第二行:每种研究材料的占用空间
int[] weights = new int[M+1];
for (int i = 1; i <= M; i++) {
weights[i] = sc.nextInt();
}
// 读取第三行:每种研究材料的价值
int[] values = new int[M+1];
for (int i = 1; i <= M; i++) {
values[i] = sc.nextInt();
}
// 2. 定义一维dp数组,dp[j]表示容量为j时可以获取的最大价值
int[] dp = new int[N + 1];
for (int i=1;i<=M ;i++ ){
for(int j=N;j>=weights[i];j--){
dp[j]=Math.max(dp[j], dp[j - weights[i]] + values[i]);
}
}
System.out.println(dp[N]);
}}1、分割等和子集
https://leetcode.cn/problems/partition-equal-subset-sum/description/
class Solution {
public boolean canPartition(int[] nums) {
int len=nums.length;
int sum=0;
for (int i = 0; i <len ; i++) {
sum+=nums[i];
}
if(sum%2!=0)
return false;
int res=sum/2;
int[] dp=new int[res+1];
for (int i = 0; i < len; i++) {
for (int j = res; j >=nums[i] ; j--) {
dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
}
if(dp[res]==res){
return true;
}
}
return false;
}
}2、最后一块石头的重量II
https://leetcode.cn/problems/last-stone-weight-ii/description/
class Solution {
public int lastStoneWeightII(int[] stones) {
int len=stones.length;
int sum=0;
for (int i = 0; i <len ; i++) {
sum+=stones[i];
}
int res=sum/2;
int[] dp=new int[res+1];
for (int i = 0; i < len; i++) {
for (int j = res; j >=stones[i] ; j--) {
dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum-2*dp[res];
}
}尽可能的分配 比如说总和为11 那么我们希望 dp[5] 即总和5尽可能的装石头 看总和5 最大的石头数为多少,之后再用总和减。
3、目标和
https://leetcode.cn/problems/target-sum/description/
class Solution {
public int res=0;
public int findTargetSumWays(int[] nums, int target) {
int sum=0;
for (int i = 0; i <nums.length ; i++) {
sum+=nums[i];
}
if(sum<Math.abs(target)) return 0;
if((sum+target)%2!=0) return 0;
int res=(sum+target)/2;
int[] dp=new int[res+1];
dp[0]=1;
for (int i = 0; i <nums.length ; i++) {
for (int j=res;j>=nums[i];j--){
dp[j]+=dp[j-nums[i]];
}
}
return dp[res];
}
}假设 正数为r 负数为l
那么 r+l=sum ①
并且 r-l=target ②
l=sum-r
带入 ② r=(sum+target)/2
如果除不尽 其实就代表不能得到target的总和。
dp[j] 表示 得到为j和的组合数
如果 j=5 那么 dp[5]=dp[4]+dp[3]+d[2]+dp[1]
比如 我们装了1 那么就是有dp[4]种方法 以此类推 这里不要+1,因为是求方法数,已经有了装满4的dp[4]种方法,在这种基础上在装1即可。
dp[j]+=dp[j-nums[i]];4、一和零
https://leetcode.cn/problems/ones-and-zeroes/description/
回溯算法做 超时了
class Solution {
private int m_count=0;
private int n_count=0;
private int res=0;
public int findMaxForm(String[] strs, int m, int n) {
if (strs.length==0)
return 0;
backtracking(strs,m,n,0,0);
return res;
}
public void backtracking(String[] strs, int m, int n,int index,int sum){
if(m_count>m||n_count>n){
return;
}
res=Math.max(res,sum);
for (int i = index; i <strs.length ; i++) {
char[] chars = strs[i].toCharArray();
for (int j = 0; j <chars.length ; j++) {
if (chars[j]=='0')
m_count++;
if (chars[j]=='1')
n_count++;
}
sum++;
backtracking(strs,m,n,i+1,sum);
for (int j = 0; j <chars.length ; j++) {
if (chars[j]=='0')
m_count--;
if (chars[j]=='1')
n_count--;
}
sum--;
}
}}dp
class Solution {
private int res=0;
public int findMaxForm(String[] strs, int m, int n) {
if (strs.length==0)
return 0;
int[][] dp=new int[m+1][n+1];
for(int i=0;i<strs.length;i++){
char[] chars = strs[i].toCharArray();
int x=0;
int y=0;
for (int j = 0; j <chars.length ; j++) {
if (chars[j]=='0')
x++;
else
y++;
}
for (int j =m ; j >=x ; j--) {
for (int k = n; k >=y; k--) {
dp[j][k]=Math.max(dp[j][k],dp[j-x][k-y]+1);
}
}
} return dp[m][n];
}
}这也是一个01背包问题,每个值只能被选择一次,不同点在于,这里有两个纬度,一个m一个n。
但是万变不离其宗,并且要注意,使用滚动数组要从右往左,因为我们依赖于上一行及其左边的值,因为上一行表示选择0-i-1,而本行表示选择0-i,如果我们不选择当前行的值,那么当前行的值应该与上一行的相同。
完全背包
//先遍历物品,再遍历背包
private static void testCompletePack(){
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWeight = 4;
int[] dp = new int[bagWeight + 1];
for (int i = 0; i < weight.length; i++){ // 遍历物品
for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
for (int maxValue : dp){
System.out.println(maxValue + " ");
}
}
//先遍历背包,再遍历物品
private static void testCompletePackAnotherWay(){
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWeight = 4;
int[] dp = new int[bagWeight + 1];
for (int i = 1; i <= bagWeight; i++){ // 遍历背包容量
for (int j = 0; j < weight.length; j++){ // 遍历物品
if (i - weight[j] >= 0){
dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);
}
}
}
for (int maxValue : dp){
System.out.println(maxValue + " ");
}
}因为可以重复选,所以我们的dp[i][j]=max(dp[i-1][j],dp[i][j-costs[i]]+val[i]) 即在选择i物品时 我们仍然可以选择这个物品
依赖的是当前行左边的 和上一行当前列 的。
所以空间压缩时,我们从左往右即可
左边 的是当前行更新的,dp[j]还没更新正好是之前的。
1、零钱兑换 II
https://leetcode.cn/problems/coin-change-ii/description/
class Solution {
public int change(int amount, int[] coins) {
if (coins.length==0){
return 0;
}
int[] dp=new int[amount+1];
dp[0]=1;
for (int i = 0; i <coins.length ; i++) {
for (int j = coins[i]; j <=amount ; j++) {
dp[j] += dp[j - coins[i]];
}
}
return dp[amount];
}
}这个不能先容量后物品,因为 先容量的话,是排列问题,
会出现1,2;2,1的情况,但是先物品,后容量就不会出现该问题。
2、组合总和 Ⅳ
https://leetcode.cn/problems/combination-sum-iv/description/
class Solution {
public int combinationSum4(int[] nums, int target) {
int[] dp=new int[target+1];
dp[0]=1;
for (int i = 0; i <=target ; i++) {
for (int j =0 ; j <nums.length ; j++) {
if(i>=nums[j])
dp[i]+=dp[i-nums[j]];
}
}
return dp[target];
}
}如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
该题是排列
3、爬楼梯
https://kamacoder.com/problempage.php?pid=1067
import java.util.*;
public class Main{
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int[] dp = new int[n+1];
dp[0]=1;
dp[1]=1;
for (int i = 2; i <=n ; i++) {
for (int j =1 ; j <=m ; j++) {
if(i>=j)
dp[i]+=dp[i-j];
}
}
System.out.println(dp[n]);
}}也是排列问题
注意初始化
3、零钱兑换
https://leetcode.cn/problems/coin-change/description/
class Solution {
public int coinChange(int[] coins, int amount) {
int max = Integer.MAX_VALUE;
int[] dp = new int[amount + 1];
//初始化dp数组为最大值
for (int j = 0; j < dp.length; j++) {
dp[j] = max;
}
dp[0]=0;
for (int i = 0; i <coins.length ; i++) {
for (int j = coins[i]; j <=amount ; j++) {
//只有不是最大值的时候 才有选择的必要 会溢出
if (dp[j - coins[i]] != max) {
//选择硬币数目最小的情况
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
}
}
}
return dp[amount] == max ? -1 : dp[amount];
}
}dp[j] 表示凑够j元的饿最小金钱的个数 所以要加1
同时因为是最小值 我们要刚开始初始化为最大值
初始化也要注意,dp[0]=0;如果有金币5,dp[5-5]虽然是0,但是由于多了一个金币,所以加1,所以数量是1,所以应该初始化为0
4、完全平方数
https://leetcode.cn/problems/perfect-squares/description/
class Solution {
public int numSquares(int n) {
int max = Integer.MAX_VALUE;
int[] dp=new int[n+1];
dp[0]=0;
for (int i = 1; i <=n ; i++) {
dp[i]=max;
}
for (int i = 1; i*i <=n ; i++) {
for (int j = i*i; j <=n ; j++) {
dp[j]=Math.min(dp[j],dp[j-i*i]+1);
}
}
return dp[n];
}
}和上一题其实是一样的,
本题相当于从正整数1,4,9.....这些中去选用最小的数量拼凑出 n
不久相当于上一题的从某些零钱中选取最小的个数拼凑出总金额amount吗,
不一样的是 这里的物品的重量相当于i*i;
5、单词拆分
https://leetcode.cn/problems/word-break/description/
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
boolean[] dp=new boolean[s.length()+1];
dp[0]=true;
//先遍历背包 在遍历物品
for (int i = 1; i <=s.length(); i++) {
for (int j = 0; j <wordDict.size() ; j++) {
String word = wordDict.get(j);
int len = word.length(); // 当前物品的长度
// 检查长度是否足够以及子串是否等于字典中的单词
if (i >= len && s.substring(i - len, i).equals(word) && dp[i - len]) {
dp[i] = true;
break;
}
}
}
return dp[s.length()];
}
}因为是求排列数 所以要先背包 后物品
这里可能会出现121 这些情况 且与112 不同
6、打家劫舍Ⅰ
https://leetcode.cn/problems/house-robber/description/
class Solution {
public int rob(int[] nums) {
if(nums.length==1) return nums[0];
int[] dp=new int[nums.length+1];
int sum=0;
for (int i = 0; i <nums.length ; i++) {
sum+=nums[i];
}
dp[0]=nums[0];
dp[1]=Math.max(nums[0],nums[1]);
for (int i = 2; i <nums.length ; i++) { //物品
dp[i]=Math.max(dp[i-2]+nums[i],dp[i-1]);
}
return dp[nums.length-1];
}
}7、打家劫舍Ⅱ
https://leetcode.cn/problems/house-robber-ii/description/
class Solution {
public int rob(int[] nums) {
if (nums == null || nums.length == 0)
return 0;
int len = nums.length;
if (len == 1)
return nums[0];
if(len==2)
return Math.max(nums[0],nums[1]);
return Math.max(robAction(nums, 0, len - 1), robAction(nums, 1, len));
}
private static int robAction(int[] nums,int start,int end) {
int[] dp=new int[nums.length];
dp[start]= nums[start];
dp[start+1]=Math.max(nums[start], nums[start+1]);
for (int i = start+2; i < end ; i++) { //物品
dp[i]=Math.max(dp[i-2]+ nums[i],dp[i-1]);
}
return dp[end-1];
}
}
8、打家劫舍Ⅲ
https://leetcode.cn/problems/house-robber-iii/description/
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int rob(TreeNode root) {
int[] res = robAction1(root);
return Math.max(res[0], res[1]);
}
int[] robAction1(TreeNode root) {
int res[] = new int[2];
if (root == null)
return new int[]{0,0};
int[] left = robAction1(root.left);
int[] right = robAction1(root.right);
res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
res[1] = root.val + left[0] + right[0];
return res;
}
}


