链表

1、环形链表

题目:https://leetcode.cn/problems/linked-list-cycle-ii/description/

①使用哈希表

public class Solution {
    public ListNode detectCycle(ListNode head) {
         Set<ListNode> visited = new HashSet<ListNode>();
         ListNode pa=head;
         while(pa!=null){
            if(visited.contains(pa)){
                return pa;
            }
            visited.add(pa);
            pa=pa.next;
         }
         return null;
    }
}

②使用快慢指针

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow=head;
        ListNode fast=head;
        while(fast!=null && fast.next!=null){
            slow=slow.next;
            fast=fast.next.next;
            if(slow==fast){
                ListNode index1=head;
                ListNode index2=slow;
                    while(index1!=index2){
                        index1=index1.next;
                        index2=index2.next;
                    }
                    return index1;
            }
        }
        return null;
    }
}

问题：

快指针每次走两步，慢指针每次走一步，为什么有环就一定会相遇？

没有环，则一定不会相遇。

有环，快指针先进入环，接着慢指针进入，快指针相当于每次以一步的速度去追赶慢指针，所以一定会相遇。

如果找到环的入口？

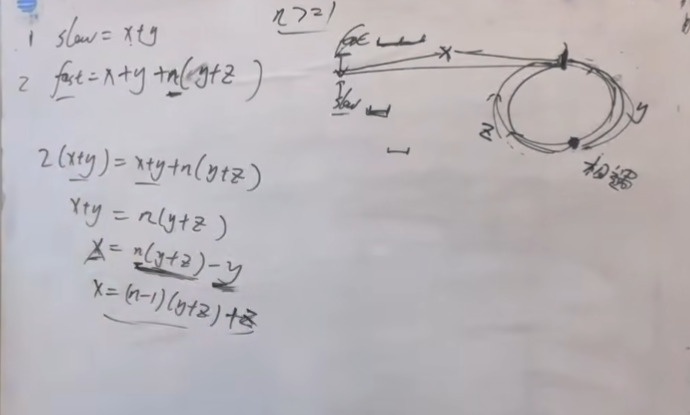
不论快指针在环里走了几圈，不论n=几 y+z都是环的距离，即最后x=z；那么当相遇时，我们设置一个从head出发，一个从相遇位置出发，则最后两个指针相遇的位置就是环的入口。

为什么慢指针走的是 x+y 而不是x+y+k（y+z）呢？即为什么慢指针在环里走不到一圈就一定会相遇。

我们可以把环摊开，

首先slow进环的时候，fast一定是先进环来了。

如果slow进环入口，fast也在环入口，那么把这个环展开成直线，就是如下图的样子：

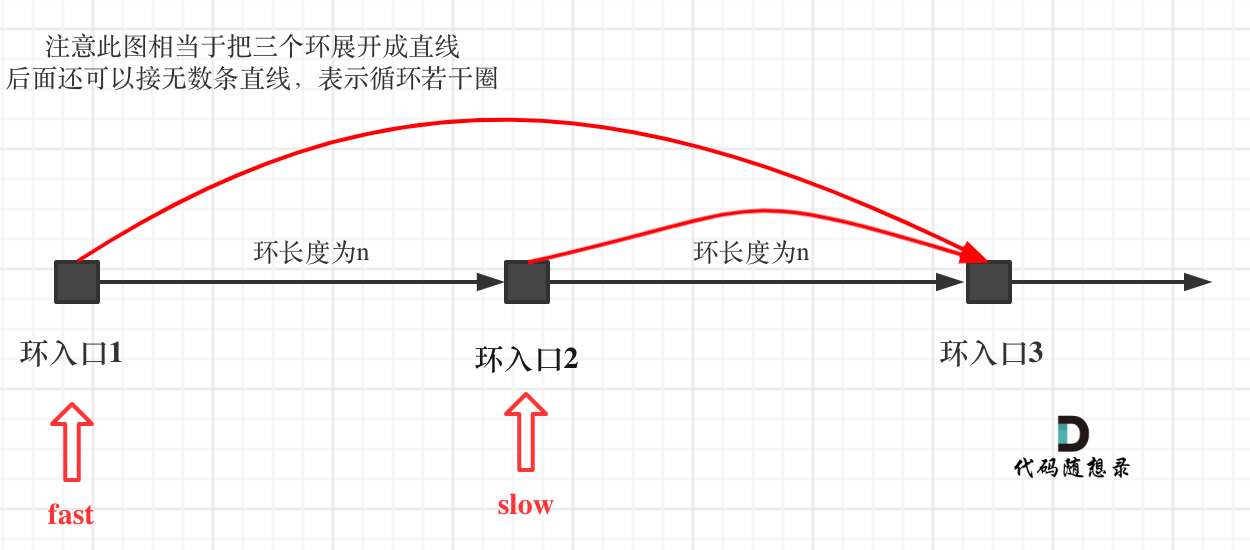
可以看出如果slow 和 fast同时在环入口开始走，一定会在环入口3相遇，slow走了一圈，fast走了两圈。

重点来了，slow进环的时候，fast一定是在环的任意一个位置，如图：

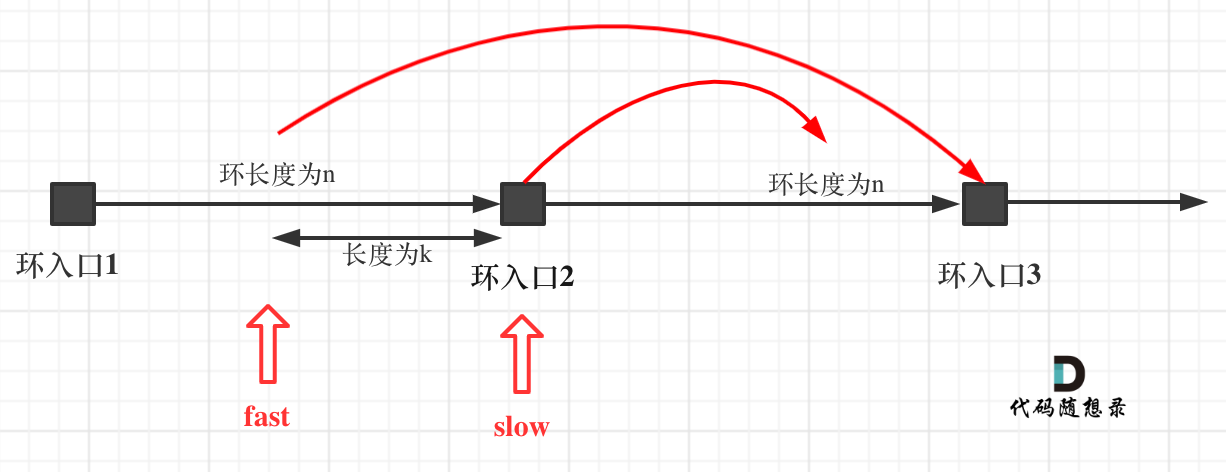
那么fast指针走到环入口3的时候，已经走了k + n 个节点，slow相应的应该走了(k + n) / 2 个节点。

因为k是小于n的（图中可以看出），所以(k + n) / 2 一定小于n。

也就是说slow一定没有走到环入口3，而fast已经到环入口3了。

这说明什么呢？

在slow开始走的那一环已经和fast相遇了。